Code
print("Hello, B.Tech Students!")Hello, B.Tech Students!Aim
This session introduces the fundamental libraries that make Python a powerhouse for engineering.
NumPy, Matplotlib, and SymPyObjective: To get comfortable creating arrays, plotting data, and performing symbolic calculations.
Python coding with colab
You can complete your experiments using colab- A cloud jupyter notebook. Please use the following link to run Python code in colab. https://colab.google/ (Right click and open in a new tab)
The classic first program for any language.
print("Hello, B.Tech Students!")Hello, B.Tech Students!Introduction to different data types like integers, floats, and strings.
x = 10 # Integer
y = 3.5 # Float
name = "Python" # String
is_student = True # Boolean
print(x, y, name, is_student)10 3.5 Python TrueUsing if, elif, and else statements.
x = 10 # Integer
if x>5:
print("x is greater than 5")
elif x==5:
print("x is 5")
else:
print("x is less than 5")x is greater than 5Using for and while loops.
# For loop
for i in range(5):
print("Iteration:", i)Iteration: 0
Iteration: 1
Iteration: 2
Iteration: 3
Iteration: 4# While loop
n = 0
while n < 3:
print("While loop iteration:", n)
n += 1While loop iteration: 0
While loop iteration: 1
While loop iteration: 2Defining and calling functions.
def add_numbers(a, b):
return a + b
result = add_numbers(5, 3)
print("Sum:", result)Sum: 8NumPyNumPy is useful for numerical operations.
#Solve 2x+3y=54x+4y=6
import numpy as np
A = np.array([[2, 3], [4, 4]])
b = np.array([5, 6])
x = np.linalg.solve(A, b)
print("Solution:", x)Solution: [-0.5 2. ]Matplotlib is used for simple visualizations. Install using: pip install matplotlib
#Plotting a sine wave
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 10, 100)
y = np.sin(x)
plt.plot(x, y)
plt.xlabel("x")
plt.ylabel("sin(x)")
plt.title("Sine Wave")
plt.show()
import numpy as np
import matplotlib.pyplot as plt
# Parameters
Vs = 5.0 # Source voltage (Volts)
R = 1000 # Resistance (Ohms)
C = 1e-6 # Capacitance (Farads)
tau = R * C # Time constant
# Create a time vector from 0 to 5*tau
t = np.linspace(0, 5 * tau, 100)
# Calculate voltage using the formula
Vc = Vs * (1 - np.exp(-t / tau))
# Plotting the result
plt.figure(figsize=(8, 5))
plt.plot(t, Vc, label=f'RC = {tau}s')
plt.title('Capacitor Charging Voltage')
plt.xlabel('Time (s)')
plt.ylabel('Voltage (V)')
plt.grid(True)
plt.legend()
plt.show()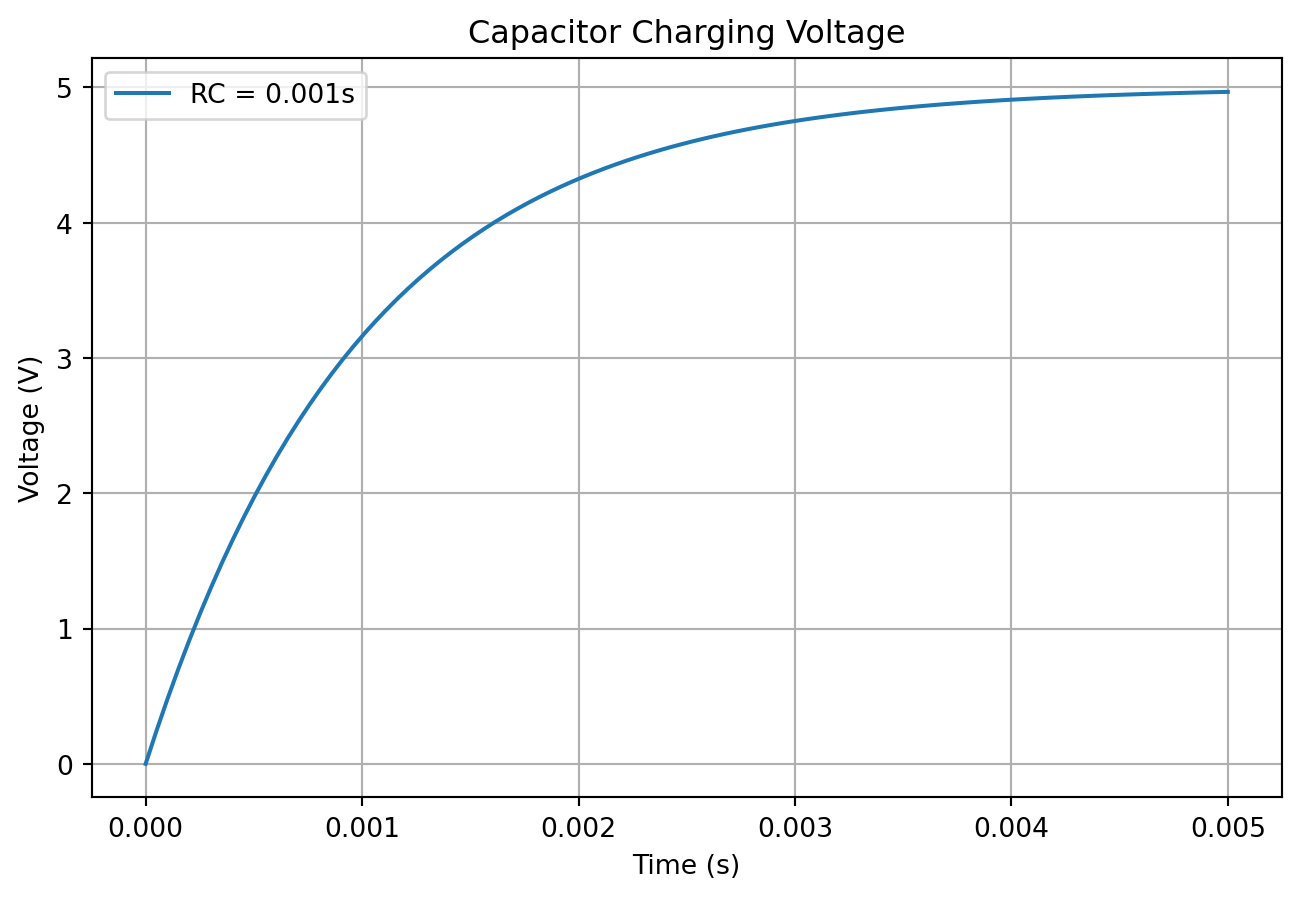
SciPy provides numerical solvers for differential equations and optimizations.
Scipy
The Scipy library can be installed using the pip install scipy command in terminal or using !pip install scipy in colab.
#Solving a Simple PDE ∂u/∂x + ∂u/∂t=0
from sympy import symbols, Function, Eq, Derivative, pdsolve
# Define variables
x, t = symbols('x t')
u = Function('u')(x, t)
# Define a simple PDE: ∂u/∂x + ∂u/∂t = 0
pde = Eq(Derivative(u, x) + Derivative(u, t), 0)
# Solve the PDE using pdsolve
solution = pdsolve(pde)
# Print the solution
print(solution)Eq(u(x, t), F(-t + x))# Example: Solving an ODE as an approximation for a PDE
from scipy.integrate import solve_ivp
import numpy as np
from scipy.integrate import solve_ivp
import numpy as np
import matplotlib.pyplot as plt
def pde_rhs(t, u):
return -0.5 * u # Example equation
sol = solve_ivp(pde_rhs, [0, 10], [1], t_eval=np.linspace(0, 10, 100))
plt.plot(sol.t, sol.y[0])
plt.xlabel('Time')
plt.ylabel('Solution')
plt.show()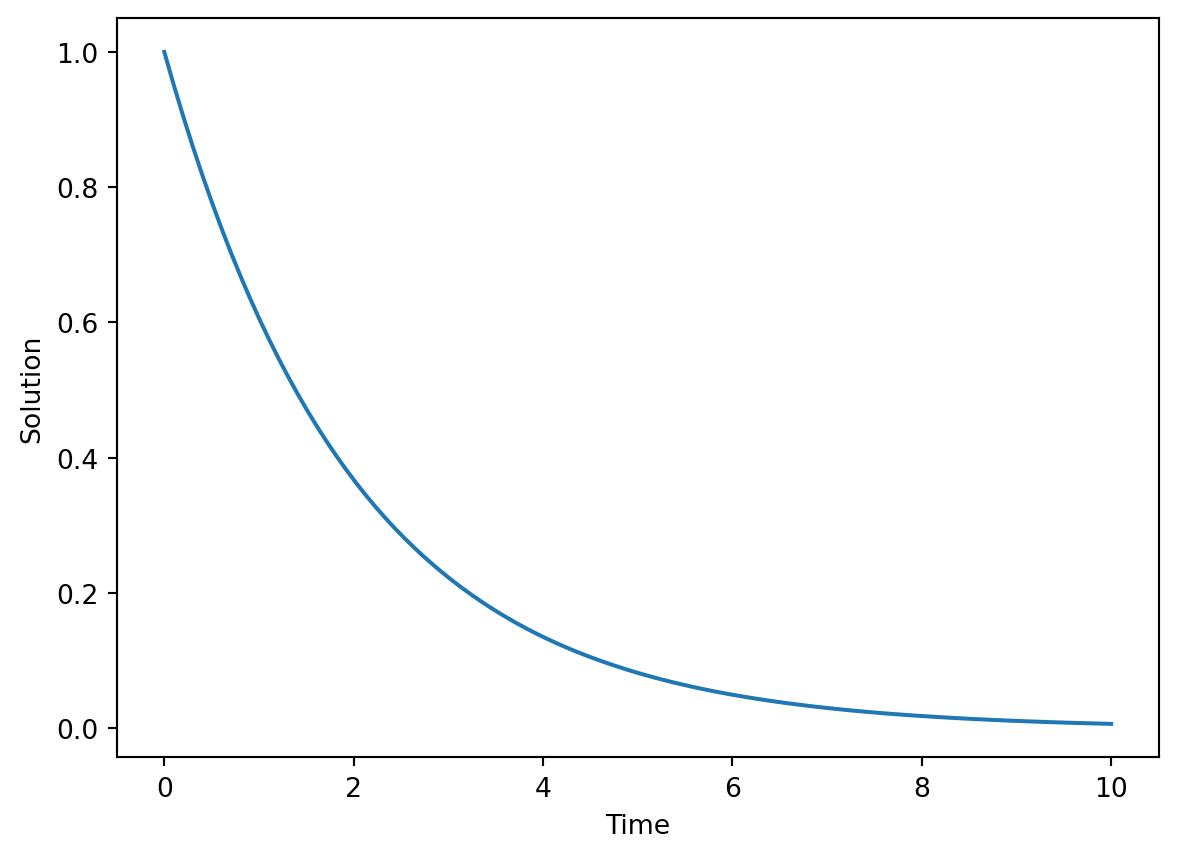
SymPySymPy is a symbolic mathematics library that can be used to derive analytical solutions to PDEs.
from scipy.optimize import minimize
def objective(x):
return x**2 + 2*x + 1
result = minimize(objective, 0) # Start search at x=0
print("Optimal x:", result.x)Optimal x: [-1.00000001]Concept: In electronics, continuous analog signals (like AC voltage) are sampled at discrete time intervals to be processed by a digital system (like a microcontroller or computer). A NumPy array is the perfect way to store these sampled values.
Python Skills: * np.linspace(): To create an array of evenly spaced time points. * np.sin(): An element-wise function that applies the sine function to every value in an array.
Task: Generate and plot a 50 Hz sine wave voltage signal with a peak voltage of 5V, sampled for 3 cycles.
import numpy as np
import matplotlib.pyplot as plt
# --- Parameters ---
frequency = 50 # Hz
peak_voltage = 5.0 # Volts
cycles = 3
sampling_rate = 1000 # Samples per second
# --- Time Array Generation ---
# Duration of 3 cycles is 3 * (1/frequency)
duration = cycles / frequency
# Create 1000 points per second * duration
num_samples = int(sampling_rate * duration)
t = np.linspace(0, duration, num_samples)
# --- Signal Generation ---
# The formula for a sine wave is V(t) = V_peak * sin(2 * pi * f * t)
voltage = peak_voltage * np.sin(2 * np.pi * frequency * t)
# --- Visualization ---
plt.figure(figsize=(10, 4))
plt.plot(t, voltage)
plt.title('Digital Representation of a 50 Hz Sine Wave')
plt.xlabel('Time (s)')
plt.ylabel('Voltage (V)')
plt.grid(True)
plt.show()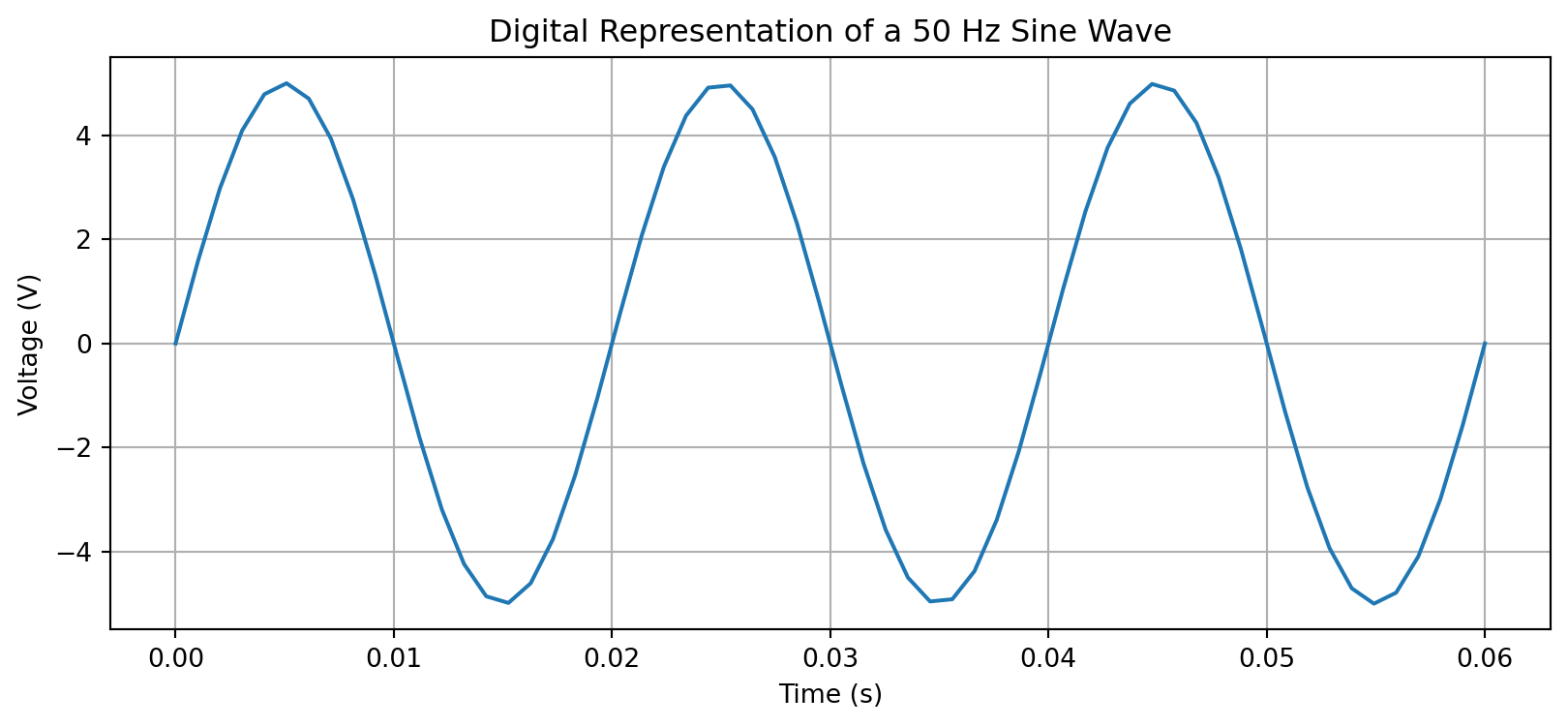
Concept: Real-world sensor data is never perfect. It’s often corrupted by random noise. We can simulate this by adding a random component to our ideal signal.
Python Skills: - Array Addition: Simply using + to add two arrays of the same shape.
np.random.normal(): To generate Gaussian noise, which is a common model for electronic noise.Task: Take the 5V sine wave from the previous example and add Gaussian noise with a standard deviation of 0.5V to simulate a noisy sensor reading.
# We can reuse the 't' and 'voltage' arrays from the previous example
noise_amplitude = 0.5 # Standard deviation of the noise in Volts
# Generate noise with the same shape as our voltage array
noise = np.random.normal(0, noise_amplitude, voltage.shape)
# Create the noisy signal by adding the noise to the ideal signal
noisy_voltage = voltage + noise
# --- Visualization ---
plt.figure(figsize=(10, 4))
plt.plot(t, voltage, label='Ideal Signal', linestyle='--')
plt.plot(t, noisy_voltage, label='Noisy Sensor Reading', alpha=0.75)
plt.title('Ideal vs. Noisy Signal')
plt.xlabel('Time (s)')
plt.ylabel('Voltage (V)')
plt.legend()
plt.grid(True)
plt.show()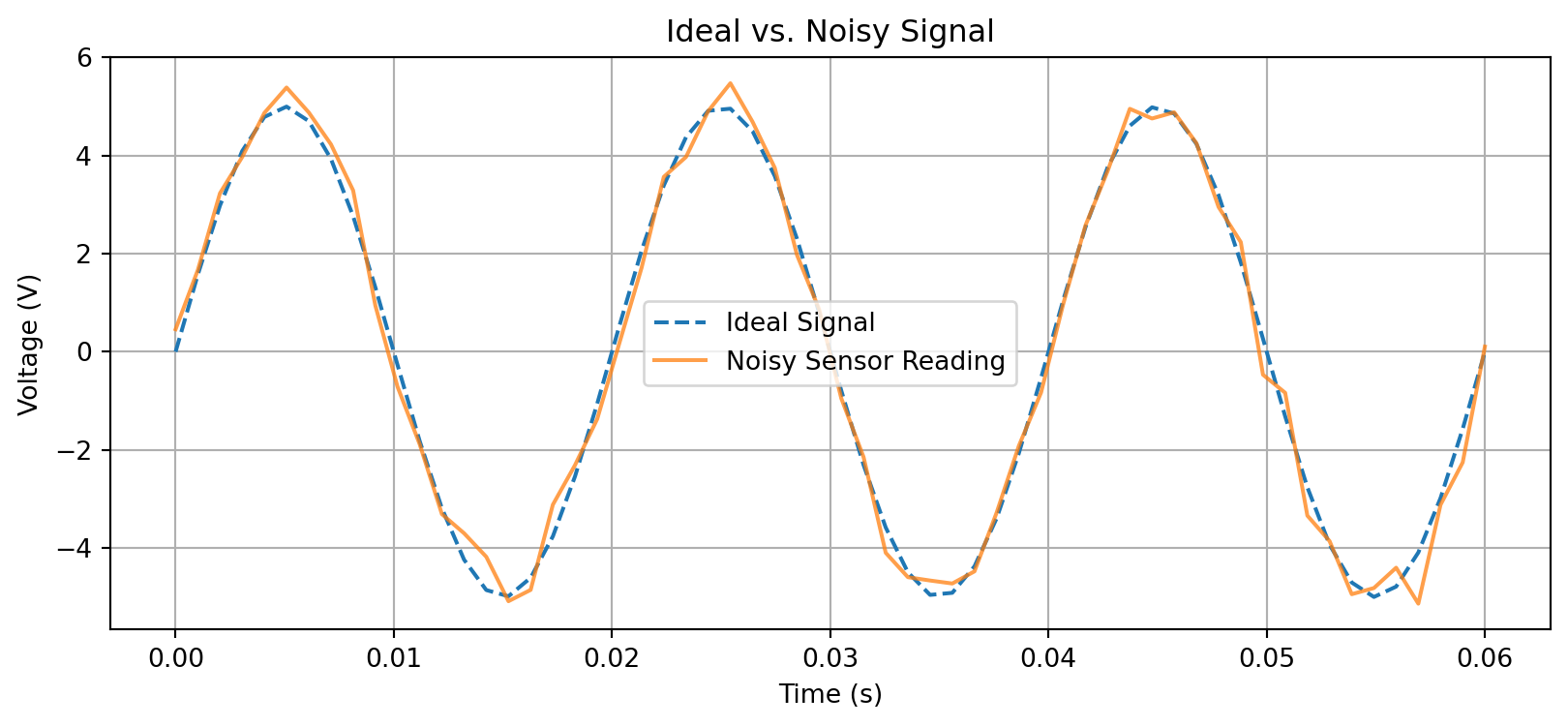
Concept: Forward kinematics in robotics is the process of calculating the position of the robot’s end-effector (e.g., its gripper) based on its joint angles. For a simple 2D arm, this involves basic trigonometry.
Python Skills:
np.cos, np.sin, np.deg2rad).Task: Calculate and plot the position of a 2-link planar robot arm with link lengths L1=1.0m and L2=0.7m for given joint angles theta1=30° and theta2=45°.
# --- Parameters ---
L1 = 1.0 # Length of link 1
L2 = 0.7 # Length of link 2
theta1_deg = 30
theta2_deg = 45
# Convert angles to radians for numpy's trig functions
theta1 = np.deg2rad(theta1_deg)
theta2 = np.deg2rad(theta2_deg)
# --- Kinematics Calculations ---
# Position of the first joint (end of L1)
x1 = L1 * np.cos(theta1)
y1 = L1 * np.sin(theta1)
# Position of the end-effector (end of L2) relative to the first joint
# The angle of the second link is theta1 + theta2
x2 = x1 + L2 * np.cos(theta1 + theta2)
y2 = y1 + L2 * np.sin(theta1 + theta2)
# --- Visualization ---
plt.figure(figsize=(6, 6))
# Plot the arm links
plt.plot([0, x1], [0, y1], 'r-o', linewidth=3, markersize=10, label='Link 1')
plt.plot([x1, x2], [y1, y2], 'b-o', linewidth=3, markersize=10, label='Link 2')
# Plot the base and end-effector positions for clarity
plt.plot(0, 0, 'ko', markersize=15, label='Base')
plt.plot(x2, y2, 'gX', markersize=15, label='End-Effector')
plt.title('2-Link Robot Arm Kinematics')
plt.xlabel('X Position (m)')
plt.ylabel('Y Position (m)')
plt.grid(True)
plt.axis('equal') # Important for correct aspect ratio
plt.legend()
plt.show()
print(f"End-effector is at position: ({x2:.2f}, {y2:.2f})")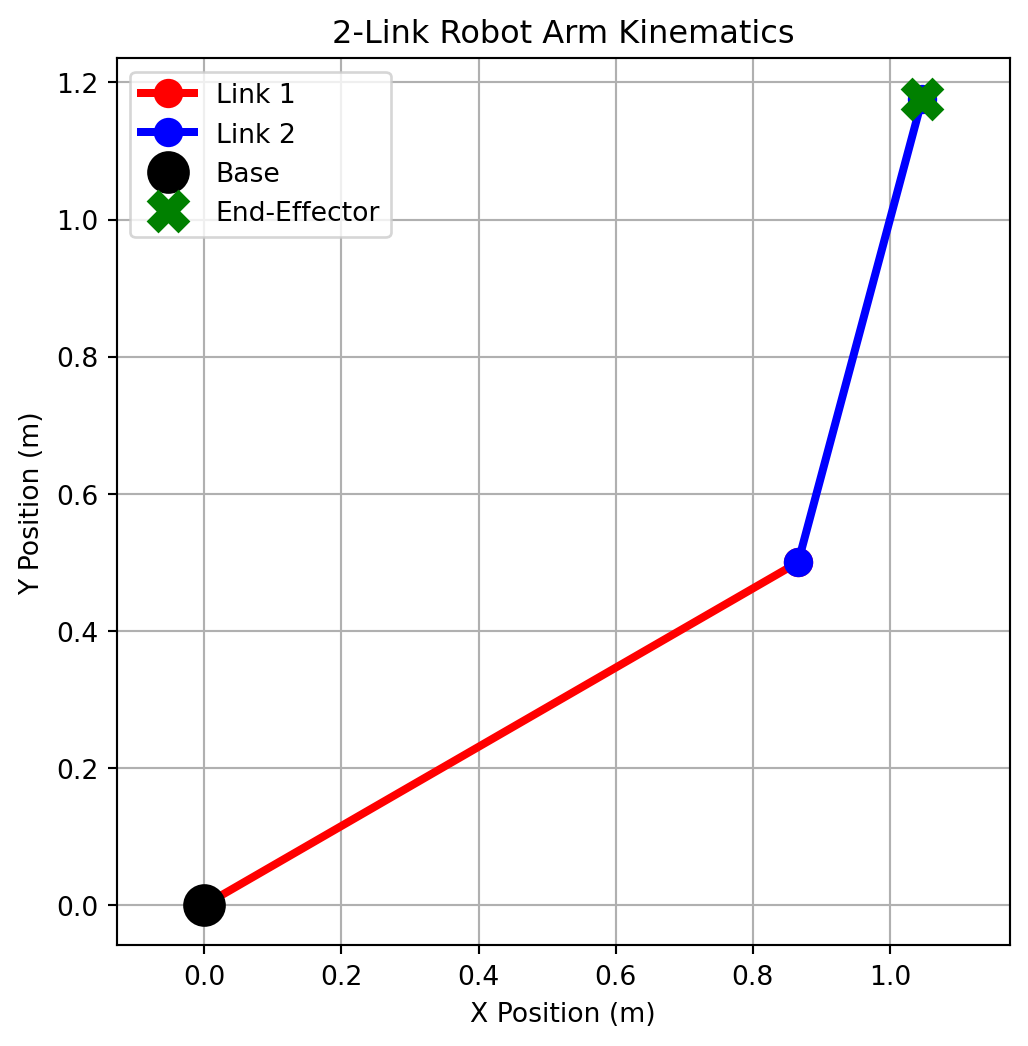
End-effector is at position: (1.05, 1.18)Concept: A robot often has sensors (like a camera or a Lidar) mounted at an angle. To understand the sensor data in the robot’s own coordinate frame, we need to rotate the data points. This is a fundamental operation in robotics and computer vision, done using a rotation matrix.
Python Skills:
Creating a 2D NumPy array (a matrix).
Matrix multiplication using the @operator.
Transposing an array (.T) for correct multiplication dimensions.
Task: A sensor detects an object at coordinates (2, 0) in its own frame. The sensor is rotated 45 degrees counter-clockwise relative to the robot’s base. Find the object’s coordinates in the robot’s frame.
# Angle of the sensor relative to the robot
angle_deg = 45
angle_rad = np.deg2rad(angle_deg)
# Point detected in the sensor's frame [x, y]
p_sensor = np.array([[2], [0]]) # As a column vector
# 2D Rotation Matrix
# R = [[cos(theta), -sin(theta)],
# [sin(theta), cos(theta)]]
R = np.array([[np.cos(angle_rad), -np.sin(angle_rad)],
[np.sin(angle_rad), np.cos(angle_rad)]])
# The transformation: p_robot = R @ p_sensor
p_robot = R @ p_sensor
# --- Visualization ---
plt.figure(figsize=(6, 6))
# Plot sensor's axes
plt.quiver(0, 0, np.cos(angle_rad), np.sin(angle_rad), color='r', scale=3, label="Sensor x'-axis")
plt.quiver(0, 0, -np.sin(angle_rad), np.cos(angle_rad), color='g', scale=3, label="Sensor y'-axis")
# Plot the point in the robot's frame
plt.plot(p_robot[0], p_robot[1], 'bo', markersize=10, label='Point in Robot Frame')
# For context, let's show where the point was in the sensor's frame (if it weren't rotated)
# This is just for visualization
plt.plot(p_sensor[0], p_sensor[1], 'ko', markersize=10, alpha=0.5, label='Original point (relative to axes)')
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.grid(True)
plt.axis('equal')
plt.xlim(-1, 3)
plt.ylim(-1, 3)
plt.title("Coordinate Frame Rotation")
plt.xlabel("Robot X-axis")
plt.ylabel("Robot Y-axis")
plt.legend()
plt.show()
print("Rotation Matrix:\n", np.round(R, 2))
print(f"\nPoint in Sensor Frame: {p_sensor.flatten()}")
print(f"Point in Robot Frame: {np.round(p_robot.flatten(), 2)}")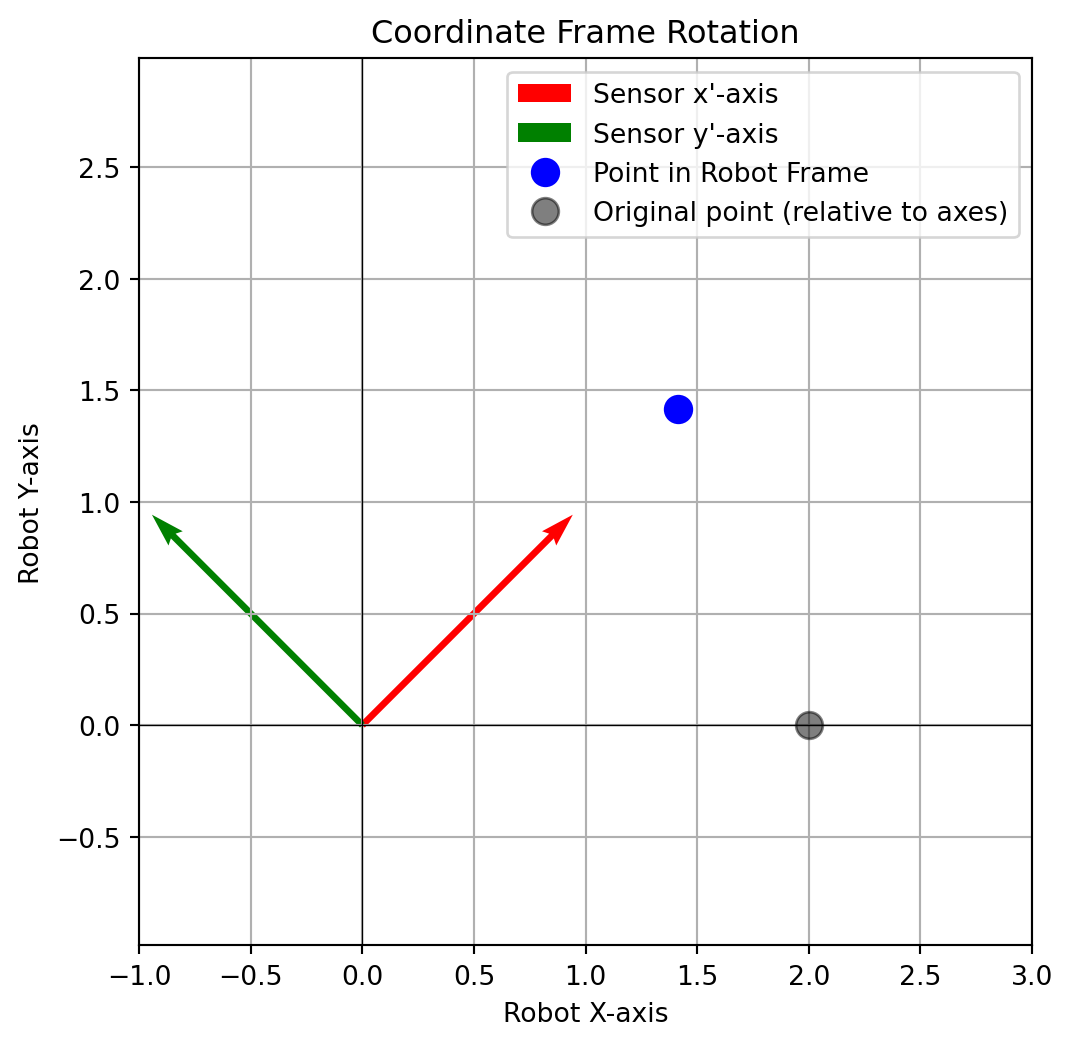
Rotation Matrix:
[[ 0.71 -0.71]
[ 0.71 0.71]]
Point in Sensor Frame: [2 0]
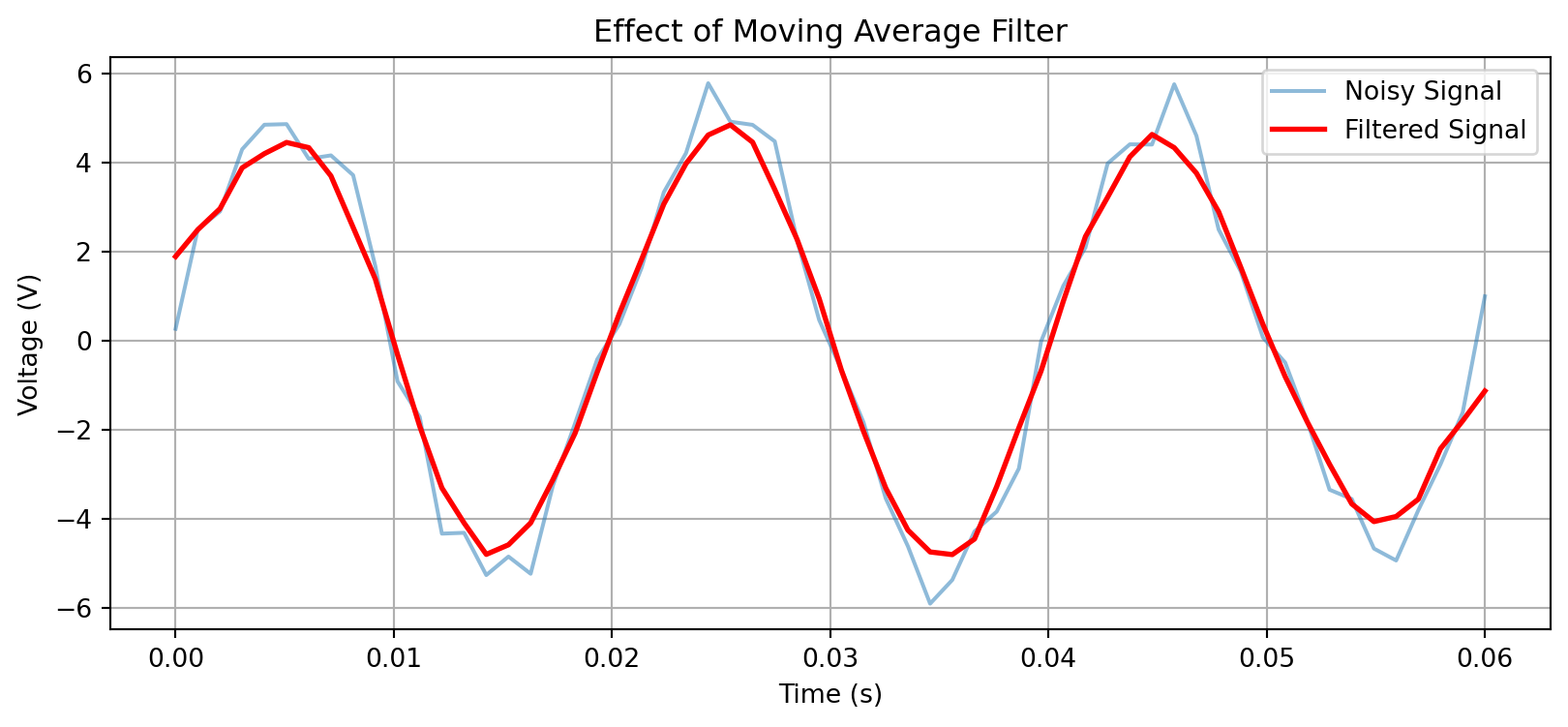
Point in Robot Frame: [1.41 1.41]Concept: To clean up the noisy signal from Example 3, we can apply a digital filter. The simplest is a moving average filter, which replaces each data point with the average of itself and its neighbors. This smooths out sharp fluctuations (noise).
Python Skills:
np.mean(): To calculate the average of a set of numbers.Task: Apply a 5-point moving average filter to the noisy_voltage signal created in Example 3 and plot the result to see the smoothing effect.
# Let's regenerate the noisy signal for a self-contained example
# (In a real notebook, you would reuse the variable from before)
frequency = 50
peak_voltage = 5.0
duration = 3 / frequency
t = np.linspace(0, duration, int(1000 * duration))
voltage = peak_voltage * np.sin(2 * np.pi * frequency * t)
noise = np.random.normal(0, 0.5, voltage.shape)
noisy_voltage = voltage + noise
# --- Filtering ---
window_size = 5
# Create an empty array to store the filtered signal
filtered_voltage = np.zeros_like(noisy_voltage)
# Loop through the signal. We can't compute a full window at the very edges,
# so we'll just copy the original values for the first and last few points.
for i in range(len(noisy_voltage)):
# Find the start and end of the slice
start = max(0, i - window_size // 2)
end = min(len(noisy_voltage), i + window_size // 2 + 1)
# Get the window of data and calculate its mean
window = noisy_voltage[start:end]
filtered_voltage[i] = np.mean(window)
# --- Visualization ---
plt.figure(figsize=(10, 4))
plt.plot(t, noisy_voltage, label='Noisy Signal', alpha=0.5)
plt.plot(t, filtered_voltage, label='Filtered Signal', color='r', linewidth=2)
plt.title('Effect of Moving Average Filter')
plt.xlabel('Time (s)')
plt.ylabel('Voltage (V)')
plt.legend()
plt.grid(True)
plt.show()